Null and Alternative Hypothesis Examples | Null Hypothesis and Alternative Hypothesis Examples

Null and Alternative Hypothesis Examples: A Comprehensive Guide

When conducting scientific research or statistical analysis, two of the most fundamental concepts you’ll encounter are the null hypothesis and the alternative hypothesis. Understanding these hypotheses and how to apply them is essential for testing theories, evaluating research questions, and drawing valid conclusions. In this comprehensive guide, we will define what null and alternative hypotheses are, explore examples, and walk you through how to write and apply them in different research contexts.

What is a Null Hypothesis?

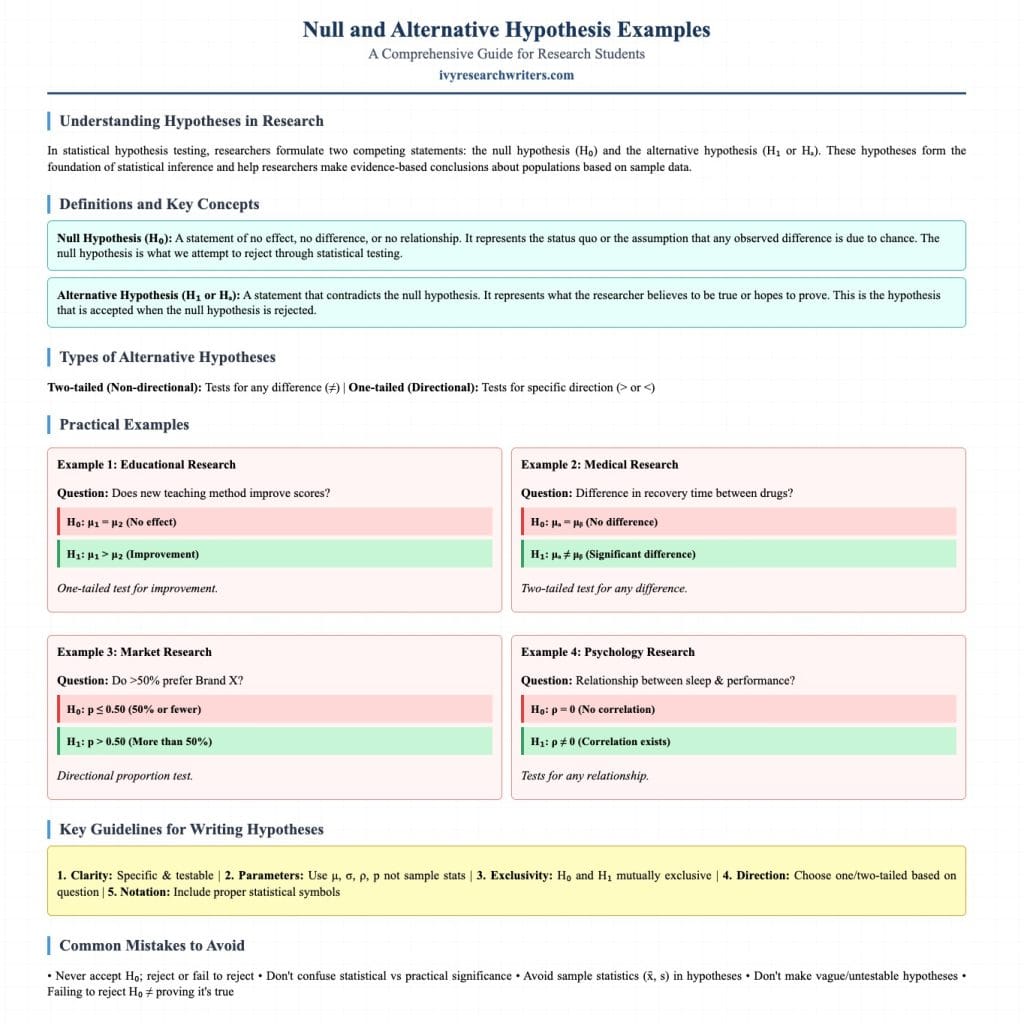
The null hypothesis (H₀) is a statement that suggests there is no significant effect or relationship between the variables being studied. Essentially, it asserts that any observed difference or relationship in the sample data is due to random chance or sampling error, rather than a true underlying effect. The null hypothesis serves as a starting point in hypothesis testing, and its purpose is to be tested and either rejected or failed to be rejected based on evidence provided by the data.

The null hypothesis is typically structured in a way that there is no difference or no association between the variables of interest.

What is an Alternative Hypothesis?

The alternative hypothesis (H₁ or Ha) posits that there is a significant effect or relationship between the variables being studied. It contradicts the null hypothesis and suggests that the observed data or phenomenon is not the result of random chance. The alternative hypothesis is what researchers often want to prove, as it supports the research question or claim that the investigator is exploring.

While the null hypothesis assumes no effect or relationship, the alternative hypothesis is the statement that a researcher hopes to support with their study. It might suggest a difference, a relationship, or some form of impact.

Null and Alternative Hypothesis Examples: A Deeper Look

Let’s explore null and alternative hypothesis examples to better understand how they function in research.

Example 1: Testing a New Drug’s Effect on Blood Pressure

Research Question: Does the new drug reduce blood pressure in patients?

• Null Hypothesis (H₀): The new drug does not reduce blood pressure in patients. This null hypothesis suggests that there is no effect of the drug on blood pressure, and any observed changes could be attributed to chance or other factors.
• Alternative Hypothesis (H₁): The new drug does reduce blood pressure in patients. Here, the alternative hypothesis suggests that the drug has a significant effect on lowering blood pressure, which is what the researchers are trying to prove.

In this example, a statistical test (e.g., a t-test or ANOVA) would be used to analyze the data. If the test shows a p-value less than a predefined significance level (typically 0.05), the null hypothesis is rejected, and the alternative hypothesis is accepted, meaning the drug likely reduces blood pressure.

Example 2: Comparing Test Scores Between Two Groups

Research Question: Do students who use a study app perform better on their exams compared to students who do not use the app?

• Null Hypothesis (H₀): There is no difference in test scores between students who use the study app and those who do not.
• Alternative Hypothesis (H₁): Students who use the study app perform better on their exams than those who do not.

In this case, the null hypothesis suggests that the app has no impact on exam scores, while the alternative hypothesis suggests the app improves performance. Researchers would collect data on the test scores of both groups and perform a statistical test (such as a two-sample t-test) to evaluate whether the difference in scores is statistically significant.

Example 3: Evaluating a New Teaching Method

Research Question: Does the new teaching method improve student engagement?

• Null Hypothesis (H₀): The new teaching method does not improve student engagement compared to the traditional method.
• Alternative Hypothesis (H₁): The new teaching method improves student engagement compared to the traditional method.

Here, the null hypothesis assumes that there is no difference in student engagement between the two teaching methods, while the alternative hypothesis suggests that the new method is more effective. Statistical analysis would be used to test whether the data supports the alternative hypothesis or whether the null hypothesis cannot be rejected.

How to Write Null and Alternative Hypotheses

Writing null and alternative hypotheses requires a systematic approach. Here’s how to structure them:

1. Clearly define the research question: Your hypothesis should directly address the research question. For instance, if you want to test whether a new product increases sales, your hypotheses will focus on the relationship between product usage and sales.
2. State the null hypothesis: The null hypothesis is often a statement of no effect or no relationship. Use words like no difference, no effect, or no relationship to clearly communicate this assumption. Example: “There is no relationship between the amount of exercise and weight loss in adults.”
3. State the alternative hypothesis: The alternative hypothesis should represent the opposite of the null hypothesis, proposing that there is a relationship or effect. Example: “There is a relationship between the amount of exercise and weight loss in adults.”
4. Choose the type of hypothesis test: Depending on the nature of your research question, choose whether to conduct a one-tailed or two-tailed hypothesis test. A one-tailed test looks for an effect in one direction (greater than or less than), while a two-tailed test looks for an effect in both directions (greater than or less than).

The Importance of Hypothesis Testing in Research

Hypothesis testing is a critical component of scientific research. It allows researchers to evaluate the null hypothesis and determine if there is enough evidence to reject the null hypothesis. By rejecting the null hypothesis, researchers can support the alternative hypothesis, thus making a meaningful contribution to their field of study.

Key points in hypothesis testing include:

• The null hypothesis is assumed to be true unless the hypothesis test provides enough evidence to reject it.
• The alternative hypothesis is supported when there is enough evidence to suggest that the null hypothesis is false.
• Statistical tests (such as t-tests, chi-square tests, or ANOVA) provide the framework for hypothesis testing, allowing researchers to make decisions based on sample data.

Parameter: Understanding the Role of Parameters in Hypothesis Testing

A parameter in hypothesis testing refers to a numerical characteristic of a population that we are interested in estimating or testing. For example, the population parameter might refer to the mean or proportion of a specific group or population. When conducting a hypothesis test, you often compare sample data against this parameter to determine whether the sample provides enough evidence to support or reject a particular hypothesis.

In hypothesis testing, we start by formulating two hypotheses about the population parameter:

• The null hypothesis (H₀) usually asserts that the population parameter equals a specific value, indicating no effect or relationship.
• The alternative hypothesis (H₁) states that the population parameter differs from that value, implying that there is an effect or relationship.

For example, when testing if a new medicine reduces cholesterol, the population parameter would be the average reduction in cholesterol levels across the entire population, and the null hypothesis (H₀) might state that the mean cholesterol reduction is equal to 0, while the alternative hypothesis (H₁) would propose that the mean cholesterol reduction is not 0.

Hypothesis States: How to Properly Define Hypotheses

When creating a hypothesis, it is essential that the hypothesis states a clear claim about the population parameter. The null hypothesis (H₀) typically proposes that there is no effect, no difference, or no relationship between the variables in question. On the other hand, the alternative hypothesis (H₁) suggests that there is a significant effect or relationship.

For example:

• Null Hypothesis (H₀): The new medicine does not reduce cholesterol.
• Alternative Hypothesis (H₁): The new medicine reduces cholesterol.

This hypothesis states that the population parameter (e.g., cholesterol reduction) does not change due to the intervention, versus a claim that it does.

Accept the Alternative Hypothesis: When to Accept the Alternative Hypothesis

In hypothesis testing, you accept the alternative hypothesis when the null hypothesis (H₀) is rejected due to sufficient evidence from the sample data. This usually happens when the p-value from the hypothesis test is below the chosen significance level (often 0.05). By rejecting the null hypothesis, you are effectively stating that the evidence supports the alternative hypothesis.

For example, if testing whether a new medicine reduces cholesterol, you would accept the alternative hypothesis if the evidence suggests a statistically significant reduction in cholesterol after using the medicine.

H₀: The Null Hypothesis and Its Role in Testing

The null hypothesis (H₀) is a fundamental concept in hypothesis testing. It is generally stated as the assumption that there is no effect or no relationship between variables. The null hypothesis is called the null hypothesis because it represents the “status quo” or the baseline condition of the variables. The purpose of hypothesis testing is to determine whether the sample data provides enough evidence to reject the null hypothesis.

In some cases, the null hypothesis might be that the population parameter is equal to a specific value (e.g., the average cholesterol reduction is 0), or it could be that there is no difference between groups. If the hypothesis test shows otherwise, you may reject the null hypothesis and accept the alternative hypothesis.

≠: Understanding the Use of “Not Equal” in Hypothesis Testing

In hypothesis testing, the symbol ≠ denotes “not equal to.” When formulating the alternative hypothesis, it is often the case that you are testing whether a parameter is not equal to a specific value. This can be a two-tailed hypothesis test, where you are testing for both directions of an effect (either greater than or less than).

For example:

• Null Hypothesis (H₀): The mean cholesterol reduction is equal to 0 (μ = 0).
• Alternative Hypothesis (H₁): The mean cholesterol reduction is not equal to 0 (μ ≠ 0).

This setup indicates that you are testing whether the new medicine has any effect—either reducing or increasing cholesterol levels—rather than assuming the effect is in a specific direction.

Hypothesis Should State: Crafting a Clear Hypothesis

A well-defined hypothesis should state a clear claim that can be tested with data. It should be specific and address the key question of your research. Hypotheses must contain opposing viewpoints: the null hypothesis and the alternative hypothesis offer two different explanations for the research question, with the null hypothesis suggesting no effect, and the alternative hypothesis suggesting a significant effect.

For instance:

• Null Hypothesis (H₀): There is no difference in cholesterol reduction between two medications.
• Alternative Hypothesis (H₁): There is a difference in cholesterol reduction between the two medications.

The hypothesis should state exactly what you are testing, whether it’s a difference, a relationship, or a change in a population parameter.

Alternative Hypothesis States: The Case for Change or Difference

The alternative hypothesis states that there is a significant effect or difference in your study. Unlike the null hypothesis, which suggests no effect, the alternative hypothesis posits that something has changed, or that a relationship exists between variables. The alternative hypotheses are contradictory to the null hypothesis, making them two opposing statements that are tested during hypothesis testing.

For example:

• Null Hypothesis (H₀): There is no effect of the new diet on weight loss.
• Alternative Hypothesis (H₁): The new diet reduces weight.

The alternative hypothesis states that there is an effect, and this is the hypothesis you are trying to prove or support through your research.

Proof by Contradiction: Why Hypothesis Testing Is Not About Proof

Proof by contradiction is a method in hypothesis testing where you assume the null hypothesis is true and then try to reject the null hypothesis by showing that this assumption leads to a contradiction with the observed data. However, hypothesis testing is based on probability, not proof. Rather than proving a hypothesis true, you test whether there is enough evidence to reject the null hypothesis.

Null Hypothesis and Accept: When the Null Hypothesis Is True

Sometimes, null hypothesis is not rejected and we must accept the null. This happens when the p-value is above the critical threshold (typically 0.05), and we do not have enough evidence to reject the null hypothesis. This does not mean the null hypothesis is true, but rather that there is insufficient evidence to support the alternative hypothesis.

Hypotheses Contain Opposing Viewpoints: Exploring Two Types of Hypotheses

In hypothesis testing, hypotheses contain opposing viewpoints: the null hypothesis suggests no effect, while the alternative hypothesis suggests an effect. These alternative hypotheses are contradictory in nature, as they propose different outcomes for the research question. The goal of hypothesis testing is to determine which of these two opposing viewpoints is supported by the sample data.

Determined Which Hypothesis the Sample Information Favors

When conducting hypothesis testing, the goal is to determine which hypothesis the sample data favors. Statistical tests analyze the data and provide a p-value that helps decide whether to reject the null hypothesis or fail to reject the null hypothesis. The sample information might show that there is enough evidence to reject the null and support the alternative hypothesis, or it may show that there is insufficient evidence to reject the null hypothesis.

In conclusion, null and alternative hypotheses play a pivotal role in hypothesis testing. Understanding how to state and test these hypotheses is essential for analyzing data and making informed decisions in scientific and academic research. The process begins by formulating hypotheses, continues with hypothesis testing, and concludes by evaluating whether the data provides enough evidence to reject the null hypothesis or accept the alternative hypothesis.

At IvyResearchWriters.com, we can help you write null and alternative hypotheses, conduct hypothesis tests, and interpret your research findings effectively. Contact us today to get expert guidance on your research journey!

Final Thoughts

Null and alternative hypothesis examples illustrate the foundational concepts in hypothesis testing. By clearly defining the null hypothesis (H₀) and alternative hypothesis (H₁), researchers set the stage for investigating their research questions and drawing evidence-based conclusions. Remember, the null hypothesis represents the status quo or no effect, while the alternative hypothesis suggests a significant change or effect.

Whether you are testing a new drug, comparing two teaching methods, or evaluating the relationship between two variables, formulating and testing null and alternative hypotheses is essential to conducting sound, rigorous research.

At IvyResearchWriters.com, we specialize in helping students, researchers, and academics develop well-structured research hypotheses and assist with statistical analysis. If you need support in writing null and alternative hypotheses or conducting hypothesis testing, contact us today to get expert help!

Further Insights into Hypothesis Testing

Hypothesis testing involves statistical procedures to assess whether the null hypothesis can be rejected based on sample data. Here are some key terms and concepts:

• Reject the null hypothesis: If the evidence from the sample is strong enough, the null hypothesis can be rejected in favor of the alternative hypothesis. This is done when the p-value is below a specified threshold (typically 0.05).
• Fail to reject the null: If the evidence is not strong enough to reject the null hypothesis, then we fail to reject the null. This means there is insufficient evidence to support the alternative hypothesis.
• Evidence to reject the null: If your statistical test shows a p-value that is less than 0.05, you may have enough evidence to reject the null hypothesis and support the alternative hypothesis.
• Testing is based on probability: Hypothesis testing involves evaluating the probability of observing a result given that the null hypothesis is true. If this probability is very low, it suggests that the null hypothesis is unlikely, and the alternative hypothesis might be more plausible.
• Type I Error: This occurs when you incorrectly reject the null hypothesis when it is actually true.
• Type II Error: This occurs when you fail to reject the null hypothesis when it is actually false.

Conclusion

The null hypothesis and alternative hypothesis are essential components of hypothesis testing. They provide opposing statements that can be tested through statistical methods to help answer your research questions. By formulating clear and precise hypotheses, you can determine whether there is enough evidence to support your research hypothesis or fail to reject the null.

 FAQs about Null and Alternative Hypothesis Examples

What is a Null Hypothesis and Alternative Hypothesis Example?

A null hypothesis (often represented as H₀) is a statement that assumes there is no significant effect or relationship between variables. In contrast, the alternative hypothesis (represented as H₁) posits that there is a significant effect or relationship. The purpose of hypothesis testing is to evaluate whether the sample data provides enough evidence to reject the null hypothesis.

Example:

• Null Hypothesis (H₀): A new medicine doesnot reduce cholesterol by 25%.
• Alternative Hypothesis (H₁): A new medicine does reduce cholesterol by 25%.

In this example, the null hypothesis assumes no change, while the alternative hypothesis suggests that there is an effect (reduction in cholesterol levels).

How to Write a Null and Alternative Hypothesis Statement?

To write null and alternative hypotheses, follow these steps:

1. Identify the Research Question: The hypothesis begins by considering two hypotheses that relate to your research question. The null hypothesis assumes no effect or no relationship between the variables, while the alternative hypothesis assumes a relationship or effect exists.
2. State the Null Hypothesis (H₀): The null hypothesis is usually a statement of no effect. It suggests that any difference or relationship found in the sample is due to random chance or sampling error.
   • Example: H₀: There is no difference in test scores between students who use the study app and those who do not.
3. State the Alternative Hypothesis (H₁): The alternative hypothesis is often the hypothesis you are trying to prove. It suggests that a significant relationship or difference exists.
   • Example: H₁: Students who use the study app score higher on the test than those who do not.
4. Determine Directionality: Decide if you want to test for a one-tailed or two-tailed hypothesis. A two-tailed test checks for differences in either direction (greater than or less than), while a one-tailed test checks for a difference in one specific direction (greater than or less than).
5. Use Statistical Tests: After formulating your hypotheses, you can perform a statistical test to determine if sample information favors the alternative hypothesis. This may include using probability distribution and p-value to evaluate if the test statistic falls within the rejection region.

What Are Your Null and Alternative Hypotheses?

When designing a study, your null and alternative hypotheses should clearly outline the relationship between variables that you are testing. Here’s an example to illustrate:

Research Question: Does a new dietary supplement reduce blood pressure in patients with hypertension?

• Null Hypothesis (H₀): The dietary supplement does not reduce blood pressure in patients with hypertension.
• Alternative Hypothesis (H₁): The dietary supplement reduces blood pressure in patients with hypertension.

In this case, the null hypothesis assumes no effect, and the alternative hypothesis suggests a significant effect.

What is an Example of H₀ and H₁ Hypothesis?

The H₀ (null hypothesis) and H₁ (alternative hypothesis) are typically opposing viewpoints that allow researchers to test whether they have enough evidence to reject the null hypothesis. Hypothesis testing is based on probability laws, and researchers use statistical methods to determine which hypothesis is more likely given the data.

Example:

Let’s say you are studying the relationship between exercise and weight loss:

• Null Hypothesis (H₀): Exercise has no effect on weight loss.
• Alternative Hypothesis (H₁): Exercise reduces weight.

In this case, H₀ assumes no effect of exercise, while H₁ suggests that exercise will lead to weight loss.

You will then perform a hypothesis test to determine whether you reject the null hypothesis (if the evidence from your data is strong enough to support H₁) or fail to reject the null (if the evidence doesn’t support a significant effect of exercise on weight loss).